Trig IDs that you MUST know....and how to use them to figure out the others...
THE ONES YOU MUST MEMORIZE!!!

- #1-4 are the very basic building blocks. There is no way around knowing them.
- #5 is the basic Pythagorean Identity. It is CRAZY COMMON...you're going to see it...A LOT...don't forget it. The big thing is that it's based on the UNIT CIRCLE where the x-coordinate is the cosine and the y-coordinate is the sine and the hypotenuse is 1. thus you get that x^2 + y^2 = 1. TADA!
- For #6 and #7 I remember the following phrases: #6: "Sin-Cos-Cos-Sin-Keep the Sign" and #7: "Cos-Cos-Sin-Sine-Change the Sign" to help me remember them.
- You can actually get #8 and #9 from #6 and #7 respectively if you make both U and V equal theta (since theta plus theta is TWO THETA) but these two come up often enough that it is really worth your time to memorize them.
USING #5 TO FIGURE OUT ANOTHER PYTHAGOREAN IDENTITY (PART 1)
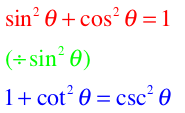
- For some reason, my brain has always seemed incapable of memorizing this (BLUE) trig ID. I think it's because there's no need to waste the brain space.
- Memorize the basic Pythagorean ID and then just divide EVERYBODY by sine squared to get this new one.
USING #5 TO FIGURE OUT ANOTHER PYTHAGOREAN IDENTITY (PART 2)
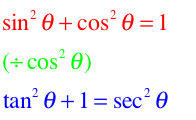
- For some reason, my brain has always seemed incapable of memorizing this (BLUE) trig ID. I think it's because there's no need to waste the brain space.
- Memorize the basic Pythagorean ID and then just divide EVERYBODY by cosine squared to get this new one.
AN ALTERNATE FORM OF THE COSINE DOUBLE ANGLE FORMULA
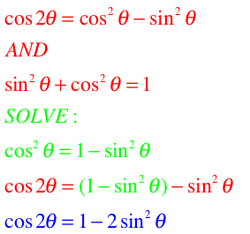
- Solve #5 for cosine squared.
- Use substitution to replace the cosine squared in #9.
- Clean up the nonsense. TADA!
ANOTHER ALTERNATE FORM OF THE COSINE DOUBLE ANGLE FORMULA
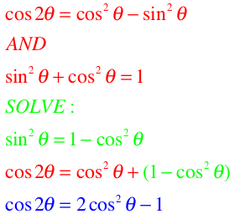
- Solve #5 for sine squared.
- Use substitution to replace the sine squared in #9.
- Clean up the nonsense. TADA!
YO! You MUST memorize the Unit Circle. It'll save your life, bro.
Really, though, the UNIT CIRCLE is like your BFF. No joke.
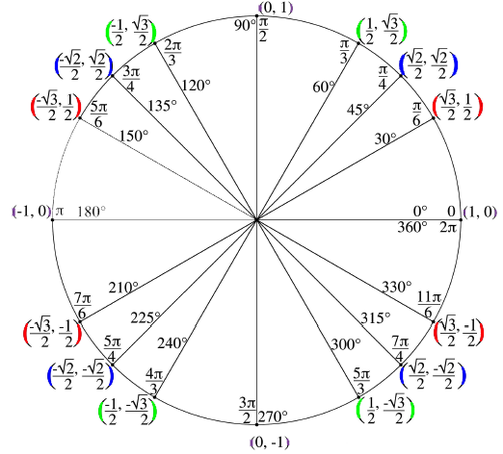
- I know it feels counter intuitive, but you will really be better at the unit circle if you think in RADIANS, not DEGREES.
- Let's start with Quadrant I. If you can memorize the points in this quadrant, you can figure out ALL of the points in the other quadrants. I've highlighted the points in different colors. Notice that all of the RED points (the pi over sixes...aka the 30 degrees) have the same basic coordinates (they only vary in terms of positives and negatives depending on the quadrant.) The same is true of the BLUE points (the pi over fours...aka the 45 degrees) and of all the GREEN points (the pi over threes...aka the 60 degrees.)
- The points on this circle serve a purpose. The x-coordinate at a particular angle is the COSINE of that angle and the y-coordinate is the SINE of that angle. I always memorize that the sin(pi/6) = 1/2 and, from that, I can fill out the rest of circle.
- The purpose of the unit circle is that you are going to be required OFTEN in your mathematics career to evaluate the six trig functions at these common angles WITHOUT A CALCULATOR. With some cleverness (and knowledge of both 30-60-90 triangles and 45-45-90 triangles) you can figure all of this out...but it will slow you down so much that you will be unlikely to finish in a suitable time frame.
- The angles IN DEGREES: Most people don't struggle too much with the degrees. I remember the pattern: "Add 30, 15, 15, 30...30, 15, 15, 30...etc." Meaning that if you start at 0 degrees (the positive x-axis) and add those values, in that order, you can work your way around the entire circle. You should end up with 360 degrees being the same as 0 degrees. If you don't, you did something incorrectly.
- The angles in RADIANS: You should be able to easily memorize the "corners" (yes, i know it's a circle...shut it...by "corners" I mean the points on the axes.) Beyond that, you need to find a system that works for you. The pi over fours are all the odd numbers over 4. So they are (in order going counterclockwise) pi/4, 3pi/4, 5pi/4, and 7pi/4. The pi over sixes are pi/6, 5pi/6, 7pi/6, and 11pi/6. (NOTE that these are all numerators that are one more or one less than a multiple of 6.) The pi over threes are also all one more or one less than a multiple of three...so pi/3, 2pi/3, 4pi/3, and 5pi/3.
