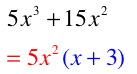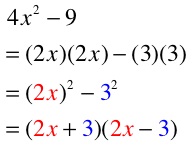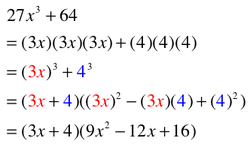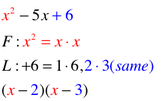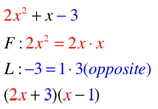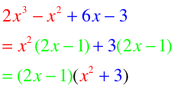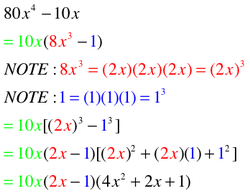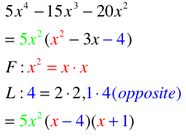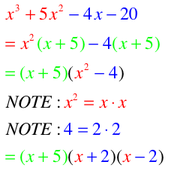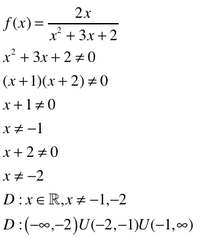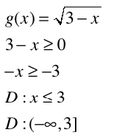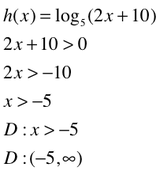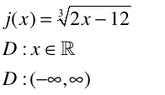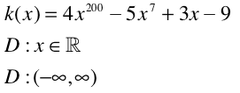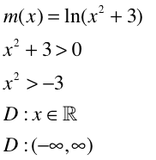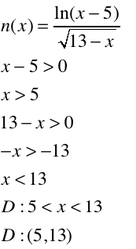Algebra Skills

OMG ,THIS PROBLEM IS EVERYWHERE:
Write the equation of a line given some info...

OPTION 1: Slope-Intercept Form (y= mx + b)
(this is like the "swiss army knife" of linear equations...ALWAYS a useful option...ALWAYS works...but NOT ALWAYS the best/fastest tool for a particular situation

This is a FOUR STEP process...if you can ALWAYS follow these four steps when asked to find a linear equation from given info.
STEP ONE: Find the slope. Depending on the info, there are a number of different ways to do this....

The slope is given (ex. "a line with a slope of 5")...congrats...FOUND IT.
Given two points. (ex. (1, 2) and (4, 1)) Use slope = (Y2-Y1)/(X2-X1)
The line is PARALLEL to a given line. (So it has the SAME SLOPE as that given line.
The line is PERPENDICULAR to a given line. (So you need to "FLIP SLOPE. CHANGE SIGN" because the slopes of perpendicular lines are opposite reciprocals.)

STEP TWO: Rewrite your equation with the correct numerical value for m.
STEP THREE: Plug in a point (x.y) that is on the line for x and y. Solve for b.
STEP FOUR: Rewrite your final answer as an equation with the correct numerical values for m and b. (Note that x and y should still be variables in the equation...because, you know, they can VARY...hence the name.)

OPTION 2: Point-Slope Form (Y - Y1 = m(X-X1))
(this is like the "screwdriver" of linear equations...it's mad effective for particular tasks, but not as useful for everything.

Here, you can boil that four step process into TWO (or three if your teacher is insistent about wanting the answer in slope-intercept form) STEPS.
STEP ONE: Find slope...exactly the same as before.
STEP TWO: Use the numerical value of the slope AND the numerical point that you have to write your answer in point-slope form. BOOM! you're done.

IF your teacher insists on an answer in slope-intercept form...
OPTIONAL STEP 3: Clean up your answer from step 2 to write the equation in
y = mx + b form.

Example #1: Given the SLOPE and a POINT.

Give the equation of a line with a slope of 2 through the point (1, -5.)
OPTION 1 (Slope-Intercept Method)
y = 2x + b
-5 = 2(1) + b
-5 = 2 + b
-7 = b
y = 2x - 7 done.

OPTION 2 (Point-Slope Method)
y - (-5) = 2(x - 1)
y + 5 = 2(x - 1) BOOM! done.

Example #2: Given TWO POINTS.

Write the equation of the line through the points (2, 3) and (-2, 5).
OPTION 1 (Slope-Intercept Method)
m = (5-3)/(-2-2) = -2/4 = -1/2
y = (-1/2)x + b
5 = (-1/2)(-2) + b
5 = 1 + b
4 = b
y = (-1/2)x + 4 done.

OPTION 2 (Point-Slope Method)
m = (5-3)/(-2-2) = -2/4 = -1/2
y - 3 = (-1/2)(x - 2) or y - 5 = (-1/2)(x + 2) done.

Example #3:
Given a POINT and a LINE PARALLEL.

Write the equation of a line through (6, 1) that is parallel to 2x + 3y = 10.
First thing, you need to find the slope of the GIVEN line. Since the lines are parallel, the line that you are trying to find will have the SAME SLOPE.
2x + 3y = 10
3y = -2x + 10
y = (-2/3)x + 10/3
slope of GIVEN LINE is -2/3.
OPTION 1 (Slope-Intercept Method)
m = -2/3
y = (-2/3)x + b
1 = (-2/3)(6) + b
1 = -4 + b
5 = b
y = (-2/3)x + 5 done.

OPTION 2 (Point-Slope Method)
m = -2/3
y - 1 = (-2/3)(x - 6) done.

Example #4:
Given a POINT and a LINE PERPENDICULAR.

Write the equation of a line through the point (-3, 4) that is perpendicular to the line 3x + 5y = 8.
First thing, you need to find the slope of the GIVEN line. Since the lines are perpendicular, the line that you are trying to find will have the OPPOSITE RECIPROCAL SLOPE (aka "flip slope. change sign.").
3x + 5y = 8
5y = -3x + 8
y = (-3/5)x + 8/5
slope of GIVEN LINE is -3/5.
thus, slope of the NEW LINE is 5/3.
OPTION 1 (Slope-Intercept Method)
m = 5/3
y = (5/3)x + b
4 = (5/3)(-3) + b
4 = -5 + b
9 = b
y = (5/3)x + 9 done.

OPTION 2 (Point-Slope Method)
m = 5/3
y - 4 = (5/3)(x + 3) done.

Example #5: (Calculus Kiddos ONLY)
Given a FXN find the equation of the line TANGENT at a given POINT.

Write the equation of the line tangent to the curve f(x) = x^3 + 4x^2 + 7x - 2 at the point (1, 10.)
To find the slope of the tangent line, we will need the derivative of the function. f'(x) = 3x^2 + 8x + 7
The slope is the derivative evaluated at the given point.
m = f'(1) = 3(1) +8(1) + 7 = 18
OPTION 1 (Slope-Intercept Method)
m = 18
y = 18x + b
10 = 18(1) + b
10 = 18 + b
-8 = b
y = 18x - 8 done.

OPTION 2 (Point-Slope Method)
m = 18
y - 10 = 18(x - 1) done.

Factoring Basics...

EXPLANATIONS

There are 5 steps to factoring most things...follow the steps where appropriate and you should be just fine..
(Note that before you start, if it's an equation, you need to make sure that one side is equal to zero.)

STEP ONE: Greatest Common Factor (GCF)
STEP TWO: Is it a binomial? If so, it might be one of a few special patterns.
1. Difference of Squares (DOS): A^2 - B^2 = (A + B)(A - B)
2. Sum or Difference of Cubes
(Think "Keep the sign, change the sign, always a positive")

A. Sum of Cubes: A^3 + B^3 = (A + B)(A^2 - AB + B^2)
B. Difference of Cubes: A^3 - B^3 = (A - B)(A^2 + AB + B^2)

STEP THREE: Is it a quadratic trinomial (or a secret quadratic trinomial...more on that later)? If so, you can use product-sum (slow but effective) or educated guess-and-check (way faster once you get it down) to attempt to factor it into the PRODUCT OF TWO BINOMIALS
STEP FOUR: Are there an even number of terms? If so, try GROUPING. Remember that when grouping, the ratios of the consecutive terms within each group need to be the same...this is an easy way to quickly spot whether grouping is a waste of time.
STEP FIVE: The "Hail Mary Pass" of factoring....Synthetic Division. If you've attempted all of the other options and you still don't have your equation completely factored, this is your final shot.

Example #1: Straight-up GCF

The GCF is in RED
The "leftovers" are in BLUE

Example #2: Straight-up Difference of Squares
(Special Binomial)

Both terms are perfect squares and the terms are being subtracted, hence the "DIFFERENCE"

Example #3:
Straight-up Sum of Cubes (Special Binomial)

Both terms are perfect cubes and they are being ADDED, hence the term "SUM"
NOTE: The trinomial that you get from a sum of difference of cubes WILL NOT FACTOR. So don't bother stressing about it.

Example #4:
Straight-up Quadratic Trinomial (a=1)

Factoring a quadratic trinomial is like un-FOILing.
The "front seats" should multiply to the FIRST Term (see RED)
The "back seats" should multiply to the LAST Term (see BLUE)
Note that the sign of the last term tells you information about the signs of the "back seats"...if the LAST term is positive, then the "back seats" have to have the SAME SIGN (and you can find that sign based on the sign of the middle term.) If the LAST term is negative, then the two "back seats" must have OPPOSITE signs.

Example #5:
Straight up Quadratic Trinomial (a>1)

Again, this is un-FOILing
The "front seats" should multiply to the FIRST term (see RED)
The "back seats" should multiply to the LAST term and should have OPPOSITE signs (see BLUE)

Example #6: Straight-up Grouping

There is no GCF for all of the terms, but if you divide the terms into TWO GROUPS (the RED group and the BLUE group) then each individual group has its own GCF.
Once those GCFs are pulled out, there is a GCF blob (in GREEN) left over.
Because the blobs are identical, they are the NEW GCF for the whole expression.
Yank out the GREEN GCF and write the "left-overs" (in RED and BLUE) in the second binomial

Example #7: GCF and a SPECIAL BINOMIAL

Take out the GCF first.
Notice that the "left-overs" are a binomial and...OMG...they seem to be like totally cubic
Use the Difference of Cubes pattern
Don't forget that GCF is still chilling in front
Remember that the trinomial from the Difference of Cubes won't factor.

Example #8: GCF and a QUADRATIC TRINOMIAL

Take out the GCF first
The "left-overs" are a Quadratic Trinomial
Don't forget to leave the GCF chilling in front
Un-FOIL the Quadratic Trinomial as explained in previous examples

Example #9:
GROUPING and a SPECIAL BINOMIAL

There is no GCF but there is an even number of terms
Split the terms into TWO groups (the RED and the BLUE)
Yank a GCF out of each group. The "left-overs" form a blob (in GREEN) that is conveniently the same for both terms
The GREEN blob is the NEW GCF...yank that out of the whole thing and write the "left-overs" (in RED and BLUE) in the second binomial

Example #10:
Looks like grouping...but it's SYNTHETIC DIVISION

Example #11:
Straight-up, no option, SYNTHETIC DIVISION

FANCY FACTORING: Secret Quadratic Trinomials...Tricky.

Some expressions/equations aren't actual quadratic trinomials BUT they follow the basic pattern of a quadratic trinomial so they look like this:
A (Blob)^2 + B (Blob) + C
Where A, B, and C are coefficients and the "BLOB" could be pretty much ANY variable expression as long as both "blobs" are the same.

These can OFTEN be factored into two binomials just like a regular quadratic trinomial.
The most common examples are TRIG blobs and EXPONENTIAL blobs

Example #2: Those Blasted Trig Fxns

Example #1: A Higher Degree Polynomial

Example #3: An Exponential Says What?

Why DOMAIN is easy (using the BIG FOUR simple rules)...

THE BIG FOUR DOMAIN RULES FOR EQUATIONS

I don't care if your parents tell you that you can do anything. They are wrong. YOU CANNOT DIVIDE BY ZERO. Even Chuck Norris cannot divide by zero. WHAT TO DO? Set the denominator NOT EQUAL to zero and solve for x. You domain is all x-values EXCEPT these solutions.
The INSIDES OF EVEN ROOTS CANNOT BE NEGATIVE...this is true for the real number system...which is the system you will be using to find domain...so trust me. Sometimes, we get all tricky and throw an ODD root at you. Who cares? Don't fall for it. The rule is only for EVEN ROOTS. Odd roots have no probs whatsoever. WHAT TO DO? Set the INSIDE OF THE EVEN ROOT greater than or equal to zero. Solve for x. This solution set is your domain.
The INSIDES OF LOGARITHMS MUST BE POSITIVE...how do you know if the equation has a logarithm? Look for the word "LOG" or, if they're trying to be tricky, "LN" (which hopefully your brain reads as "natural LOG" anyway.) WHAT TO DO? Set the INSIDE OF THE LOG strictly greater than zero and solve for x. This solution set is your domain.
REAL-WORLD CONSTRAINTS (only an issue in word problems)...this means use your noggin to realize that in many word problems a whole list of values that work MATHEMATICALLY make no sense LOGICALLY. WHAT TO DO? Think logically about the restrictions that would be on your independent variable. For instance, if my x is the age of a human, we can say that the domain is likely from 0 to 100 (as you cannot have a negative age and 100 is a reasonably maximum age for most people.)

IF YOUR EQUATION DOESN'T VIOLATE ANY OF THE "BIG FOUR" THEN, BY DEFAULT, ITS DOMAIN IS ALL REAL NUMBERS. BOOM!

Example #1: You CANNOT divide by zero.

Set the denominator not equal to zero. Factor it. Solve both factors for x. The domain is all real numbers EXCEPT these two values. The parenthetical expression of the domain is also included.

Example #2: Even Root Shenanigans

Set the INSIDE of the even root greater than or equal to zero. Solve for x. This is the domain of the function. The parenthetical expression of the domain is also included.

Example #3: Everybody Hates Logs

Set the INSIDE of the log strictly greater than zero. Solve for x. This is the domain. The parenthetical expression of the domain is also included.

Example #4: Root Trickery

There is no denominator. There is no EVEN root. There is no log. It is not a word problem. BOOM! Domain is all real numbers. The parenthetical expression of the domain is also included.

Example #5: Hey, is that a Polynomial?

There is no denominator. There is no even root. There is no log. It is not a word problem. BOOM! Domain is all real numbers. The parenthetical expression of the domain is also included.

Example #6: Nobody likes a Word Problem

This should remind you a bit of a certain summer project. You put a hole in a bottle and monitor the water level over time as it drains. What is the domain of this problem? ANSWER: The experiment starts when you uncover the hole and allow the water to drain. This is time t = 0 seconds. The experiment ends when the bottle is empty (because it makes NO SENSE for you to be staring at an empty bottle and monitoring the water level.) Thus, the domain is from 0 seconds to X seconds where X is the time as which your bottle became empty. For instance, if your bottle took 35 seconds to empty, the domain would be
D: 0 seconds < x < 35 seconds or, in parenthetical notation...D: [0, 35].

Example #7: The "Sum of Squares" Trick

Ok, so 3 isn't a perfect square, so the name of this trick is a bit off...but the point is that X^2 is always either positive or zero (it can't be negative.) Thus, when you ADD something positive to X^2, you cannot possibly get a negative value. If you see this right away, you could just jump to the domain being all real numbers. If you don't, you should see it when you try to solve for x and it involves a non-real answer. The parenthetical expression of the domain is also included.

Example #8: The Perfect Storm

YIKES...there are loads of concerns here. #1, there is a denominator and it can't equal zero. However (#2) the bottom also has an even root. Thus, combining the two, instead of setting the inside of the root greater than OR EQUAL TO zero, we should just lose the "or equal to" part since the denominator can't be zero. Also, issue #3 is that the inside of the log has to be greater than zero. Thus, we get two domain restrictions. The domain is the set of numbers that meets ALL restrictions, thus the numbers between 5 and 13 exclusively. The parenthetical expression of the domain is also included.

OMG ,THIS PROBLEM IS EVERYWHERE: Write the equation of a line given some info...

OPTION 1: Slope-Intercept Form (y= mx + b) (this is like the "swiss army knife" of linear equations...ALWAYS a useful option...ALWAYS works...but NOT ALWAYS the best/fastest tool for a particular situation

OPTION 2: Point-Slope Form (Y - Y1 = m(X-X1)) (this is like the "screwdriver" of linear equations...it's mad effective for particular tasks, but not as useful for everything.